example Constant ductility response spectra

Generate the constant ductility response spectra and associated results of an earthquake suite using OpenSeismoMatlab.

Contents

Input

earthquake motions

eqmotions={'Imperial Valley'; % Imperial valley 1979
    'Kocaeli';
    'Loma Prieta';
    'Northridge';
    'San Fernando';
    'Spitak';
    'Cape Mendocino';
    'ChiChi';
    'elcentro_NS_trunc'; % Imperial valley 1940
    'Hollister';
    'Kobe'};

Set the eigenperiod range for which the response spectra will be calculated.

Tspectra=(0.08:0.08:4)';

Set critical damping ratio of the response spectra to be calculated.

ksi=0.05;

Set the target ductility (not used here)

mu=2;

Set the postyield stiffness factor for each earthquake

p=[0.02;0.01;0.02;0.01;0.01;0.01;0.02;0.01;0.01;0.01;0.01];

Extract nonlinear response spectra

sw='cdrs';

Calculation

Initialize CDRS

CDRS=cell(numel(eqmotions),1);
% Calculation of peak values
for i=1:numel(eqmotions)
    % earthquake
    data=load([eqmotions{i},'.dat']);
    t=data(:,1);
    dt=t(2)-t(1);
    xgtt=data(:,2);
    S=OpenSeismoMatlab(dt,xgtt,sw,Tspectra,ksi,mu,p(i));
    CDRS{i}=[S.Period,S.CDSd,S.CDSv,S.CDPSa,S.fyK,S.muK,S.iterK];
end

Output

Plot constant ductility spectral displacement

Fig1 = figure('units', 'centimeters', 'Position', [0,0, 20/sqrt(2), 20]);
% Scan all subplots
for i=1:numel(eqmotions)
    subplot(4,3,i)
    plot(CDRS{i}(:,1),CDRS{i}(:,2),'k','LineWidth',1);
    set(gca,'FontName','Times New Roman')
    title(eqmotions{i},'FontName','Times New Roman')
    ylabel('Sd','FontName','Times New Roman')
    xlabel('Period (s)','FontName','Times New Roman')
    axis tight
end
drawnow;
pause(0.1)

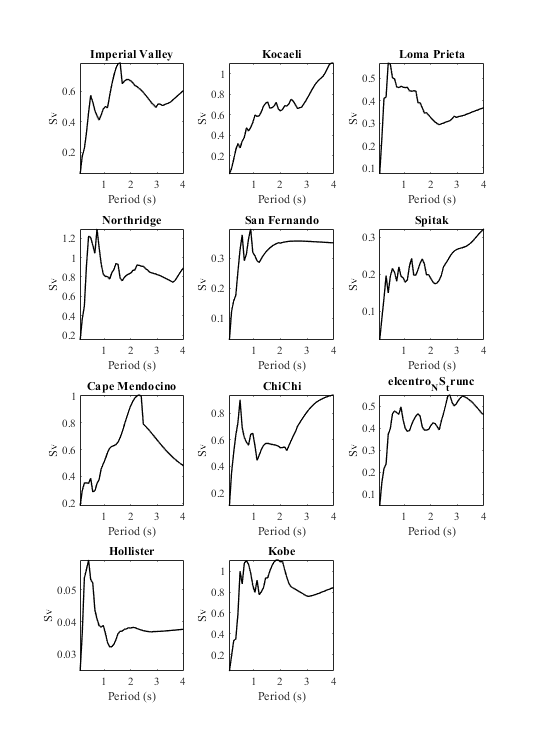
Plot constant ductility spectral velocity

Fig2 = figure('units', 'centimeters', 'Position', [0,0, 20/sqrt(2), 20]);
% Scan all subplots
for i=1:numel(eqmotions)
    subplot(4,3,i)
    plot(CDRS{i}(:,1),CDRS{i}(:,3),'k','LineWidth',1);
    set(gca,'FontName','Times New Roman')
    title(eqmotions{i},'FontName','Times New Roman')
    ylabel('Sv','FontName','Times New Roman')
    xlabel('Period (s)','FontName','Times New Roman')
    axis tight
end
drawnow;
pause(0.1)

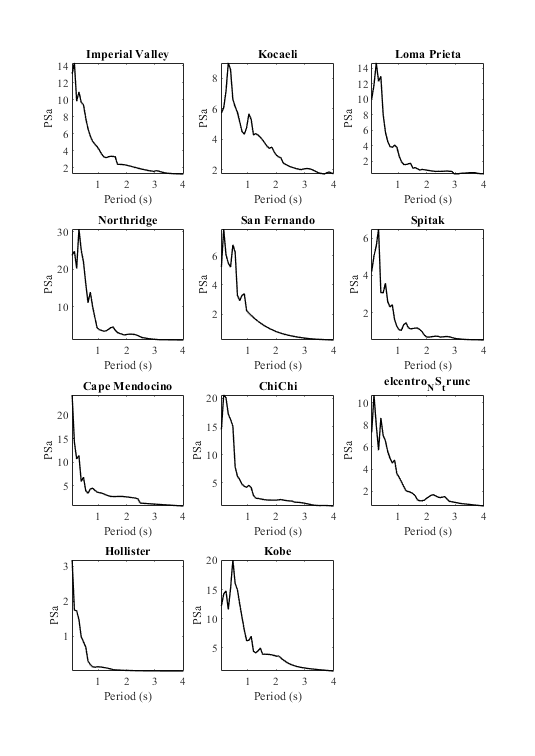
Plot constant ductility spectral acceleration

Fig3 = figure('units', 'centimeters', 'Position', [0,0, 20/sqrt(2), 20]);
% Scan all subplots
for i=1:numel(eqmotions)
    subplot(4,3,i)
    plot(CDRS{i}(:,1),CDRS{i}(:,4),'k','LineWidth',1);
    set(gca,'FontName','Times New Roman')
    title(eqmotions{i},'FontName','Times New Roman')
    ylabel('PSa','FontName','Times New Roman')
    xlabel('Period (s)','FontName','Times New Roman')
    axis tight
end
drawnow;
pause(0.1)

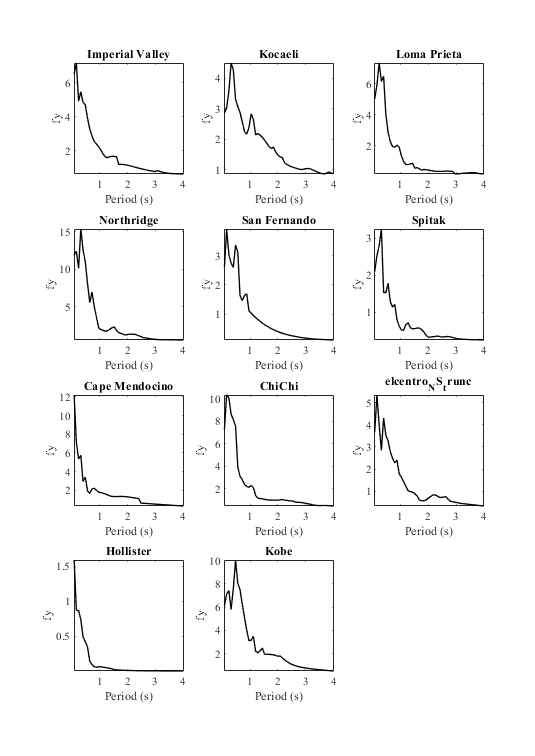
Plot constant ductility spectral yield limit

Fig4 = figure('units', 'centimeters', 'Position', [0,0, 20/sqrt(2), 20]);
% Scan all subplots
for i=1:numel(eqmotions)
    subplot(4,3,i)
    plot(CDRS{i}(:,1),CDRS{i}(:,5),'k','LineWidth',1);
    set(gca,'FontName','Times New Roman')
    title(eqmotions{i},'FontName','Times New Roman')
    ylabel('fy','FontName','Times New Roman')
    xlabel('Period (s)','FontName','Times New Roman')
    axis tight
end
drawnow;
pause(0.1)

Plot constant ductility spectral achieved ductility

Fig5 = figure('units', 'centimeters', 'Position', [0,0, 20/sqrt(2), 20]);
% Scan all subplots
for i=1:numel(eqmotions)
    subplot(4,3,i)
    plot(CDRS{i}(:,1),CDRS{i}(:,6),'k','LineWidth',1);
    set(gca,'FontName','Times New Roman')
    title(eqmotions{i},'FontName','Times New Roman')
    ylabel('mu','FontName','Times New Roman')
    xlabel('Period (s)','FontName','Times New Roman')
    axis tight
end
drawnow;
pause(0.1)

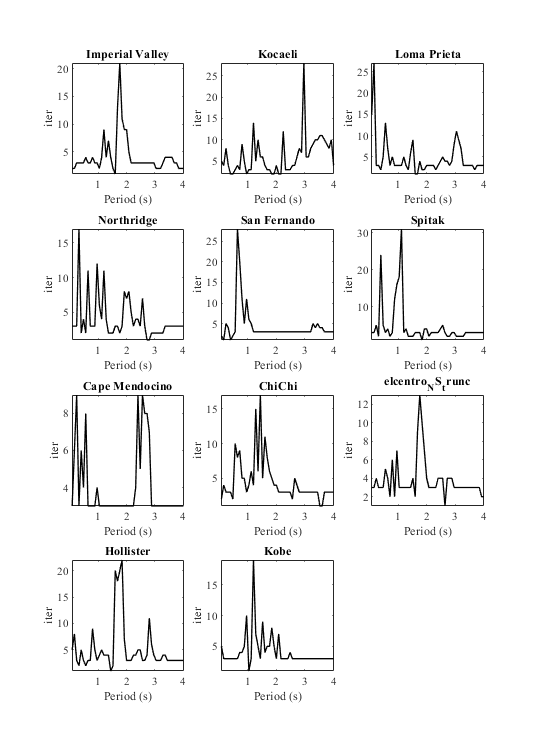
Plot constant ductility spectral number of iterations needed for convergence

Fig6 = figure('units', 'centimeters', 'Position', [0,0, 20/sqrt(2), 20]);
% Scan all subplots
for i=1:numel(eqmotions)
    subplot(4,3,i)
    plot(CDRS{i}(:,1),CDRS{i}(:,7),'k','LineWidth',1);
    set(gca,'FontName','Times New Roman')
    title(eqmotions{i},'FontName','Times New Roman')
    ylabel('iter','FontName','Times New Roman')
    xlabel('Period (s)','FontName','Times New Roman')
    axis tight
end
drawnow;
pause(0.1)

Copyright

Copyright (c) 2018-2023 by George Papazafeiropoulos

Published with MATLAB® R2022b