verification Constant strength response spectrum

Reference
Description
Load earthquake data
Calculate constant strength response spectra of earthquake motion
Plot the ductility demand response spectra
Plot the displacement demand response spectra
Copyright

Reference

Tena-Colunga, A. (1999). Simplified seismic evaluation of existing structures, 8th Canadian Conference on Earthquake Engineering, Vancouver, Canada, 317-322.

Description

In the above reference, a new type of spectrum is proposed, the constant strength response spectrum (CSRS). A displacement ductility demand spectrum (DDDS) relates peak displacement ductility demands (and other important response quantities, i.e., displacements) with structural periods of nonlinear elastic-perfectly-plastic hysteretic SDOF systems with given yield strengths. Figure 1 of the above reference is verified in this example. The SDOF system has a yield strength ratio equal to V/W=0.15 and the acceleration time history of the SCT-EW component recorded during the 1985 Michoacan earthquake is considered.

Load earthquake data

Earthquake acceleration time history of the 1985 Michoacan earthquake will be used (SCT-EW component). The txt file contains the following columns: time, acceleration N-S, acceleration E-W, acceleration V

fid=fopen('sct190985.txt','r');
text=textscan(fid,'%f %f %f %f');
fclose(fid);
t=text{1,1};
dt=t(2)-t(1);
xgtt=9.81*text{1,3};

Calculate constant strength response spectra of earthquake motion

Switch

sw='csrs';

Eigenperiods

T=linspace(0.1,5,50);

Critical damping ratio

ksi=0.05;

Strength ratios

fyR=0.15;

Post-yield stiffness factor

pysf=0.001;

Apply OpenSeismoMatlab

S1=OpenSeismoMatlab(dt,xgtt,sw,T,ksi,fyR,pysf);

Plot the ductility demand response spectra

Initialize figure

figure()
% Plot the constant strength ductility demand response spectra
plot(S1.Period,S1.CSSmu, 'k-', 'LineWidth', 1)
% Finalize figure
grid on
xlabel('T (sec)')
ylabel('\mu (-)')
xlim([0,5])
ylim([0,10])
drawnow;
pause(0.1)

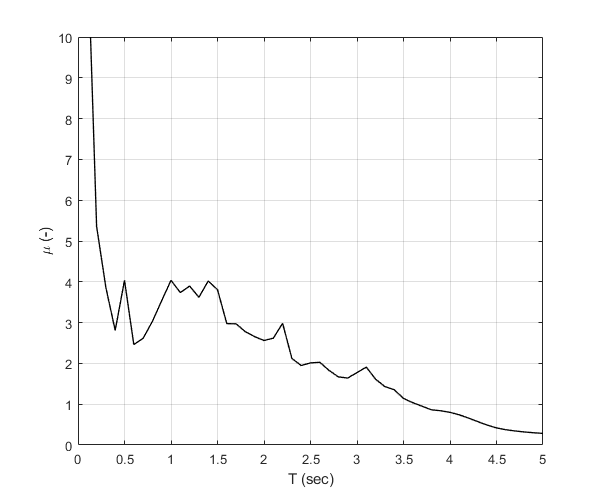
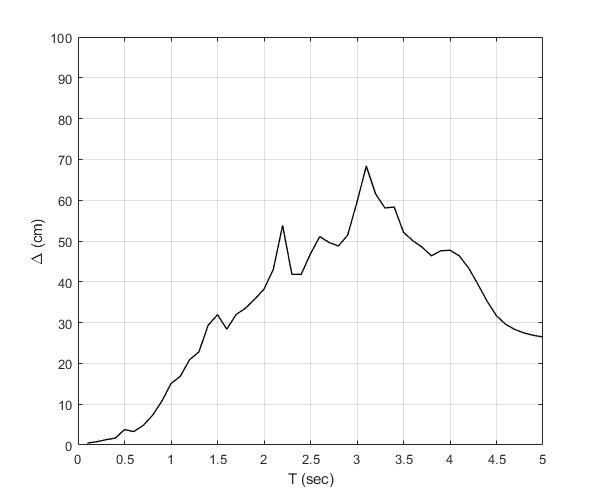
Plot the displacement demand response spectra