verification Incremental dynamic analysis of OpenSeismoMatlab

Contents

Reference

Mashayekhi, M., Harati, M., Darzi, A., & Estekanchi, H. E. (2020). Incorporation of strong motion duration in incremental-based seismic assessments. Engineering Structures, 223, 111144.

Description

Incremental dynamic analysis (IDA) is performed for a non-degrading SDOF model with eigenperiod T=1 sec. The employed hysteretic model is a bilinear elastoplastic model used for non-degrading SDOF systems and is shown in Figure 17(a) of the above reference. An IDA analysis is performed with a ground motion the spectral acceleration of which resembles the red line of Figure 14 of the above reference, i.e. the ground motion must have Sa(1 sec)=0.382g (which is the Intensity Measure - IM) and the duration D_5_75 must be roughly equal to 8.3 sec. An acceleration time history with such characteristics is shown in Figure 16(c) of the above reference. In this example, an arbitrary ground motion acceleration is loaded, which is then adjusted so that the resulting time history has Sa(1 sec)=0.382g and D_5_75=8.3 sec. The adjusted time history is plotted in this example and can be compared to Figure 16(c) of the above reference. Based on the above problem statement, the median response curve of Figure 18(a) of the above reference is verified.

Earthquake motion

Load earthquake data

eqmotions={'LomaPrietaHallsValley90'};
data=load([eqmotions{1},'.dat']);
t=data(:,1);
dt=t(2)-t(1);
xgtt=data(:,2);

Adjust earthquake motion to have D_5_75=8.3sec

Switch

sw='arias';

Apply OpenSeismoMatlab

S1=OpenSeismoMatlab(dt,xgtt,sw);

Duration D_5_75 of the initially loaded motion

S1.Td_5_75

ans =

                      7.78

S.Td_5_75 must be roughly near 8.3 sec, as required in Mashayekhi et al. (2020) We manipulate the strong shaking part of the motion which corresponds to the significant duration so that S.Td_5_75 is increased to the desired value (8.3 sec)

id1=find(t==S1.t_5_75(1));
id2=find(t==S1.t_5_75(2));
xgtt(id1:id2)=0.8*xgtt(id1:id2);

Calculate duration D_5_75 of adjusted earthquake motion

Switch

sw='arias';

Apply OpenSeismoMatlab

S2=OpenSeismoMatlab(dt,xgtt,sw);

Duration D_5_75 of the adjusted motion

S2.Td_5_75

ans =

                      7.78

Scale earthquake motion to have Sa(1 sec)=0.382g

Switch

sw='elrs';

Critical damping ratio

ksi=0.05;

Period where Sa=0.382g

T=1;

Apply OpenSeismoMatlab

S3=OpenSeismoMatlab(dt,xgtt,sw,T,ksi);

Spectral acceleration of the adjusted motion at 1 sec

S3.Sa

ans =

          1.42095612026039

Sa at 1 sec must be equal to 0.382g, so we scale the entire acceleration time history up to this level

scaleF=0.382*9.81/S3.Sa;
xgtt=xgtt*scaleF;

Calculate spectral acceleration of scaled earthquake motion

Switch

sw='elrs';

Critical damping ratio

ksi=0.05;

Period where Sa=0.382g

T=1;

Apply OpenSeismoMatlab

S4=OpenSeismoMatlab(dt,xgtt,sw,T,ksi);

Spectral acceleration of the adjusted motion at 1 sec

S4.Sa

ans =

                   3.74742

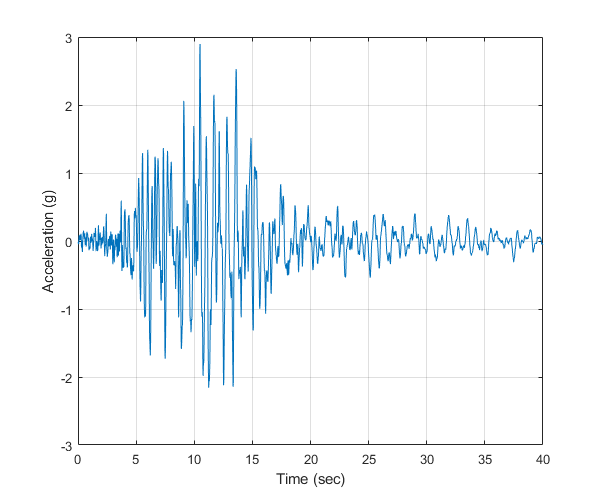
Plot the acceleration time history

Initialize figure

figure()
% Plot the acceleration time history of the adjusted motion
plot(t,xgtt)
% Finalize figure
grid on
xlabel('Time (sec)')
ylabel('Acceleration (g)')
drawnow;
pause(0.1)

Perform IDA analysis

Switch

sw='ida';

Eigenperiod

T=1;

Scaling factors

lambdaF=logspace(log10(0.001),log10(10),100);

Type of IDA analysis

IM_DM='Sa_disp';

Mass

m=1;

Yield displacement

uy = 0.082*9.81/(2*pi/T)^2;

Post yield stiffness factor

pysf=0.01;

Fraction of critical viscous damping

ksi=0.05;

Apply OpenSeismoMatlab

S5=OpenSeismoMatlab(dt,xgtt,sw,T,lambdaF,IM_DM,m,uy,pysf,ksi);

Plot the displacement time histories

Initialize figure

figure()
% Plot the response curve of the incremental dynamic analysis
plot(S5.DM*1000,S5.IM/9.81,'k','LineWidth',1)
% Finalize figure
grid on
xlabel('Displacement (mm)')
ylabel('Sa(T1,5%)[g]')
xlim([0,350])
ylim([0,0.7])
drawnow;
pause(0.1)

Copyright

Copyright (c) 2018-2023 by George Papazafeiropoulos

Published with MATLAB® R2022b