verification Strength ductility relation of elastoplastic system

Contents

Reference

Mahin, S. A., & Lin, J. (1983). Construction of inelastic response spectra for single-degree-of-freedom systems. Earthquake Engineering Center, University of California, Berkeley.

Description

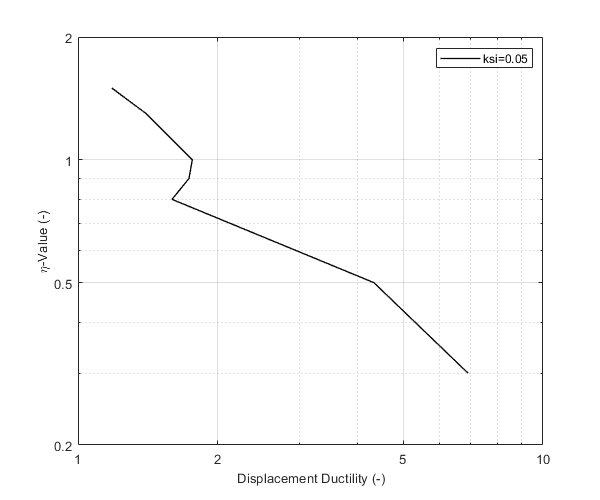
Figure 15 of the above reference is reproduced in this example, for an elastic perfectly plastic (EPP) system with eigenperiod equal to 0.7 sec and damping ratio equal to 0.05. The NS component of the El Centro earthquake (1940) is considered. It is demonstrated that there can be more than one values of strength corresponding to a given displacement ductility.

Load earthquake data

Earthquake acceleration time history of the El Centro earthquake will be used (El Centro, 1940, NS component)

fid=fopen('elcentro_NS_full.dat','r');
text=textscan(fid,'%f %f');
fclose(fid);
t=text{1,1};
dt=t(2)-t(1);
xgtt=9.81*text{1,2};

Setup parameters for NLIDABLKIN function for linear SDOF

Mass

m=1;

Eigenperiod

Tn=0.7;

Calculate the small-strain stiffness matrix

omega=2*pi/Tn;
k_hi=m*omega^2;

Assign linear elastic properties

k_lo=0.001*k_hi;

Assign yield displacement

eta=[0.3,0.5,0.8,0.9,1.0,1.3,1.5];
uy=eta*max(abs(xgtt))/k_hi;

Critical damping ratio

ksi=0.05;

Initial displacement

u0=0;

Initial velocity

ut0=0;

Algorithm to be used for the time integration

AlgID='U0-V0-Opt';

Minimum absolute value of the eigenvalues of the amplification matrix

rinf=1;

Maximum tolerance of convergence for time integration algorithm

maxtol=0.01;

Maximum number of iterations per integration time step

jmax=200;

Infinitesimal acceleration

dak=eps;

Calculate dynamic response of the linear SDOF

Apply NLIDABLKIN

mu=zeros(1,numel(uy));
for i=1:numel(uy)
[u,ut,utt,Fs,Ey,Es,Ed,jiter] = NLIDABLKIN(dt,xgtt,m,k_hi,k_lo,uy(i),...
    ksi,AlgID,u0,ut0,rinf,maxtol,jmax,dak);
    mu(i)=max(abs(u))/uy(i);
end

Plot the energy time history of the linear SDOF

Plot the damping energy and strain energy of the linearly elastic SDOF system. Convert from m to cm

figure()
loglog(mu,eta,'k','LineWidth',1)
xlim([1,10])
ylim([0.2,2])
set(gca, 'XTick', [1,2,5,10])
set(gca, 'YTick', [0.2,0.5,1,2])
xlabel('Displacement Ductility (-)','FontSize',10);
ylabel('\eta-Value (-)','FontSize',10);
grid on
legend({'ksi=0.05'})
drawnow;
pause(0.1)

Copyright

Copyright (c) 2018-2023 by George Papazafeiropoulos

Published with MATLAB® R2022b